この記事をご覧の皆様、こんにちは。
マーケティングの野崎です。
Demo3Dのカスタマイズを行う上で、プロパティを作成する(カスタムプロパティ)は必要になってくると思いますが、プロパティ作ろうと意気込んでEditCustomPropertiesを開いてType(データ型)の多さに疑問符を浮かべるDemo3D初心者の方も多いのではないでしょうか。
また、通常の開発とは異なり、3DCG特有の座標のTypeなんかもあったりします。
なので、今回はそれらのTypeを分かり易く解説していきたいと思います。
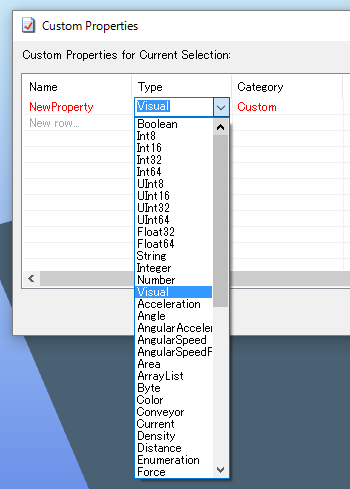
Boolean
これは普通にbool型です。通常の開発でも頻繁に利用される、trueとfalseを使った真偽の判定を行うデータ型です。
特別解説の必要も無いと思います。
integer/Int8/Int32/Int64
細かい違いが良く分からないけどとりあえずIntegerを選んでいる人も多いのではないでしょうか。
Intは整数型を取り扱う数値のデータ型です。8とか16とか32とか、後半に付随している数字はサイズを表します。
では、サイズとは何のことか?それは表示できる範囲の違いです。
Int8 : 符号付き8bit整数 (-128~127)
Int16 : 符号付き16bit整数 (-32,768~32,767)
Int32 : 符号付き32bit整数 (-2,147,483,648~2,147,483,647)
Int64 : 符号付き64bit整数 (-9,223,372,036,854,775,808~9,223,372,036,854,775,807)
8bit整数がなぜ-128~127になるのかというと、2進数で表した時8bitの最大値は11111111となります。
この2進数の値を10進数にすると、128x1+64x1+32x1+16x1+8x1+4x1+2x1+1x1=255となります。
しかし、これでは-128~127にはなりません。理由は簡単、「符号付き」8bit整数なのに符号が無いからです。
8bitの最大値の2進数である11111111に符号ビットを付けた000000000~111111111の間となるので、これを10進数に直すと-128~127という値が出てきます。
「Int8とかの計算方法は良く分からないけど、とりあえず表示できる値の大きさが違うんだな」
ということが分かって頂ければ十分です。
ところでここで疑問が生じると思いますが、このTypeの「Integer」とは何だと感じる方がいるかもしれません。
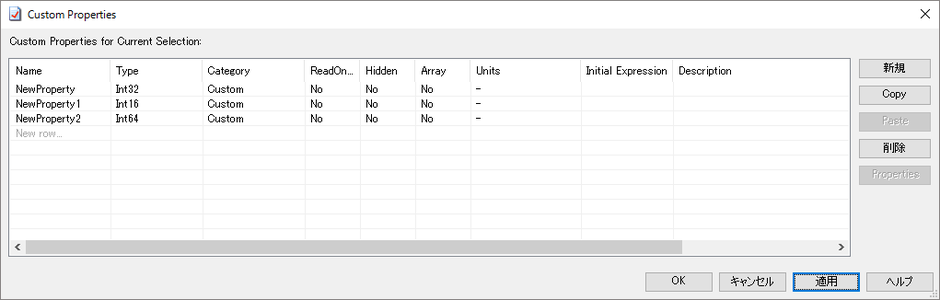
これは数字が無いだけでInt32と同様のものです。
作成して「適応」後にはIntegerで設定したプロパティはInt32に変更されているはずです。
また、ShoutはInt16、LongはInt64となります。
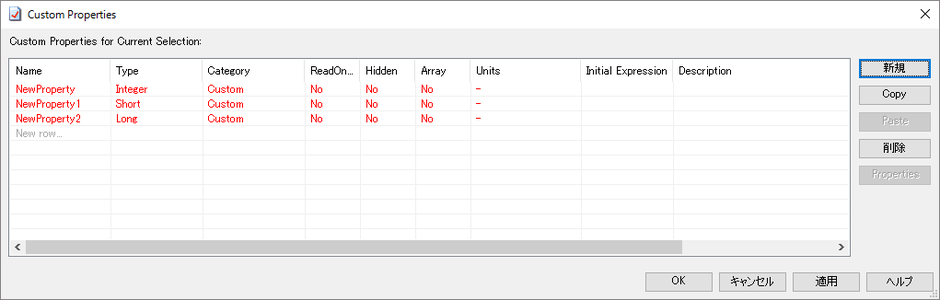
現在は千の位までしか使っていないのでInt16でいいかと安直に考えると、後々そのシステムが使われ続けて将来的にはInt32でないと!となるかもしれません。将来性を見越してデータ型を考えましょう。
UInt8/Uint16/UInt32/UInt64
今度はInt型の先頭にUが付いたものが出てきました。なんて種類が多い…。
先ほどのIntは符号付き整数型でしたが、Uが付いた場合は符号無し整数型となります。
なので-(マイナス)は無く、+のみとなります。
具体的な数値で表した場合は下記の通りです。
UInt8 : 符号無し8bit整数型 (0~255)
UInt16 : 符号無し16bit整数型 (0~65,535)
UInt32 : 符号無し32bit整数型 (0~4,294,967,295)
UInt64 : 符号無し64bit整数型 (0~18,446,744,073,709,551,615)
Float32/Float64
Floatは英語で浮く、浮遊するという意味がありますが、これは浮動小数点数型となります。
Float32 : 32bit浮動小数点数型 (1.17549e-38~3.40282e+38)
Float64 : 64bit浮動小数点数型
Float64の有効範囲はマイクロソフトのサイトにも記載が無かったので書けませんでした。Float32を使っておけばまず困る事は無いと思いますが、興味のある方はFloat64の有効範囲を計算してみてもいいかもしれないです。ただ、通常の電卓では計算出来ないのでコードを書く必要があります。
Number
Float64型と同義です。Number選択後に適用押下でFloat64に変換されます。
まとめ
細かすぎて良く分からないという人はこれさえ覚えておけば大丈夫っていうポイントまとめました。
Int 整数(+/-)
UInt 整数(+のみ)
Float 小数点数
※データ型の後ろに付く数字が大きいほど有効数値が広くなる
次回の火曜は「データ型の解説(3次元編)」です。






コメントをお書きください