2018/03/15

HDS#04 Vector3型の演算その２：位置関係

こんにちは、開発Gの杉原です。

サンプルコードの言語切り替えは自前でささっと作ったのですが、普通に不具合ありまして。

公開後すぐ直したんですが、自分もまだまだだなぁと思いました。

さて【How to Demo3D Scripting】の第四回は「Vector3型の演算その２：位置関係」をお送りします。

主にVisualの座標に使われるVector3型。

この値を使って、２つのVisualの「距離」だとか「中間地点」といったものを算出したいこともあると思います。

でも、距離の計算って自分でやろうと思うと面倒なんですよね。

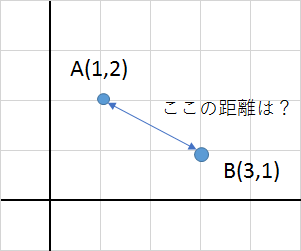
数学なんかでありがちが左の図。

A(1,2)とB(3,1)の距離を求める方法はというと、

X軸の距離 = 3 - 1 = 2

Y軸の距離 = 2 - 1 = 1

ピタゴラスの定理から

X軸の距離の2乗 + Y軸の距離の2乗 = 求めたい距離の2乗

となるので、

2^2 + 1^2 = 4 + 1 = 5

以上より、5の平方根がAB間の距離となります。

……いや、やっぱめんどくさい。何度でも言いますが、めんどくさい。

しかも、Vector3の3は3次元の3。上の図に加えてさらにZ軸の成分まで加わるので、この計算をもう1回やらなきゃいけません。

いちいち距離を求めるたびにこの計算をするコードを書くわけにはいかないですし、関数化したくなりますよね。

でもその前に、実は「2点の距離」を求める関数はないのですが、ベクトルの長さを取る関数が存在するので、それを紹介したいと思います。

JScript C#

var loc = new Vector3(2, 3, 4);
var len = loc.Length();
print(len); // 5.385165

Vector3 loc = new Vector3(2, 3, 4);
double len = loc.Length();
print(len.ToString()); // 5.385165

ここでの「長さ」とは何者かというと、原点からの距離になります。

ということは、これを使えば2点間の距離が取れるんじゃないでしょうか。

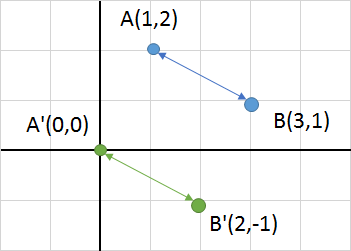
イメージとしては、こんな感じで、2点のうち一方が原点となるように移動させればいいわけです。

左図の場合、点Aが原点になるように移動させています。

移動後の座標A'とB'はそれぞれ、もととなる点A、Bに対してXを-1、Yを-2することで求めることができます。

これを3次元で、実際のDemo3Dのスクリプトで実装すると次のようになります。

JScript C#

// 2点の定義
var loc1 = new Vector3(2, 3, 4);
var loc2 = new Vector3(4, 5, 6);

// loc1が原点になるよう補正
var offset = loc2 - loc1; // 「loc2.Subtruct(loc1)」だとloc2を書き換えるので注意。第3回参照。

// 距離を算出
var len = offset.Length();

print(len); // 3.464102

// 2点の定義
Vector3 loc1 = new Vector3(2, 3, 4);
Vector3 loc2 = new Vector3(4, 5, 6);

// loc1が原点になるよう補正
Vector3 offset = loc2 - loc1; // 「loc2.Subtruct(loc1)」だとloc2を書き換えるので注意。第3回参照。

// 距離を算出
double len = offset.Length();

print(len.ToString()); // 3.464102

こんな感じで、特に難しいことを考えずに距離を求めることができました。

次は、2点の中間地点を求めたいと思います。

こちらはサクッとコードを紹介します。

JScript C#

// 2点の定義
var loc1 = new Vector3(2, 3, 4);
var loc2 = new Vector3(4, 5, 6);

// 中間地点を取得
var center = loc1.Lerp(loc2, 0.5);

print(center); // X:3 Y:4 Z:5

// 2点の定義
Vector3 loc1 = new Vector3(2, 3, 4);
Vector3 loc2 = new Vector3(4, 5, 6);

// 中間地点を取得
Vector3 center = loc1.Lerp(loc2, 0.5);

print(center.ToString()); // X:3 Y:4 Z:5

Lerp関数自体は線形補間を行い、元となる座標(例の場合loc1)から、目標の座標(例の場合loc2)までの間の座標を補間するために使います。

2つ目の引数は、2点間のどの位置を補間したいのかを0(＝0%)から1(=100%)の間の値で指定します。

この2つ目の引数に0.5(=50%)を指定することで、2点の中間地点が得られるというわけです。

さて、ここまでVector3型での距離と中間地点の求め方を紹介しましたが、１つ重大な問題があります。

Vector3型は名前の通り3次元空間ベクトルを扱っているわけですから、当然ここでいう「距離」や「中間地点」は、実際の2点のものになります。

しかし、現実的には「距離」というと、高さは考慮せず、平面的に考えることが多いと思います。

たとえばコンベアとフォークリフトの距離を求めようとします。

実際に必要なのは左図の緑色の矢印で表された距離というケースがほとんどだと思います（もっと言うと、本当ならばフォークリフトの黒い枠より外側の距離なんでしょうが）。

しかし、実際に取得されるのはオレンジの矢印で表された距離となります。

フォークリフトが上空へ飛んでいくわけがないので、こんな距離が取得できてもあまり意味が無いですね。

そこで、タイトルに「Vector3型の～」と冠しておいてなんですが、Vector3型ではない値を使って平面的に距離を取得する方法を紹介します。

使うのはVector2型、名前の通り２次元の空間ベクトルを扱うものとなります。

JScript C#

// 2点の定義
var loc1 = new Vector3(2, 3, 4);
var loc2 = new Vector3(4, 5, 6);

// Vector2化
var plan1 = new Vector2(loc1.X, loc1.Z);
var plan2 = new Vector2(loc2.X, loc2.Z);

// plan1が原点になるよう補正
var offset = plan2 - plan1;

// 距離を算出
var len = offset.Length();

print(len); // 2.828427

// 2点の定義
Vector3 loc1 = new Vector3(2, 3, 4);
Vector3 loc2 = new Vector3(4, 5, 6);

// Vector2化
Vector2 plan1 = new Vector2(loc1.X, loc1.Z);
Vector2 plan2 = new Vector2(loc2.X, loc2.Z);

// plan1が原点になるよう補正
Vector2 offset = plan2 - plan1;

// 距離を算出
double len = offset.Length();

print(len.ToString()); // 2.828427

残念ながらVector3型をVector2型に変換する仕組みは用意されていないのですが、こんな感じで平面的な距離を計算できます。

Vector2型にはLerp関数もあるので、中間地点も同様にして平面的に取得することが可能です。

Vector3型に関わる計算は結構使うことが多いのですが、こんな感じで数学の授業に出てきたような知識がなにかと必要になってきます。

正直、真面目に授業を受けていた人間ではないので、こういうことをやるたびに、真面目に勉強しておけばよかったなぁと思うわけです。

次回の【How to Demo3D Scripting】は「Vector3型の演算その３：方向」です。

更新は3/22(木)、ご期待ください。

ブログTOPに戻る